자료구조 정리 (작성중)
자료구조 정리
우리는 프로그래밍을 하면서 필요한 데이터를 int, float, String 등 다양한 형태의 변수로 저장한다. 그러나 데이터의 양이 많아질수록 이를 적절하게 관리할 방법이 필요하다. 자료구조(Data Structure)는 이런 주제를 다룬다.
자료구조란 ‘컴퓨터에 자료를 효율적으로 저장하는 방식’을 말한다. 다시 설명하자면, 자료구조는 데이터를 사용할 의도에 맞춰 적절하게 구조화하는 것을 의미한다.
예를 들어 한 학급의 학생들을 1번부터 30번까지 번호를 매겨 데이터로 저장한다고 해 보자. 우리는 이 데이터를 가지고 전체 학생 리스트를 출력하거나, 또는 특정 번호의 학생 이름을 출력하는 의도로 사용할 수 있다. 그렇다면 각각의 학생들의 번호와 이름을 별도의 변수로 저장하는 것보다는, 자료구조 중 하나인 ‘리스트’로 저장하는 게 효율적일 수 있다. 리스트를 사용하면 각 학생의 정보가 순서를 가지고 연결이 되며(그냥 변수를 만들어 저장한다면, 순서 같은 건 없을 것이다), 중간에 새로운 학생의 정보를 넣거나 기존의 학생 정보를 지우는 것도 간단해진다. 리스트에서는 그런 기능을 구현해둘 수 있기 때문이다.
자료구조를 사용하는 것은 다양한 장점을 가진다. 프로그래머가 자료를 다루기 더 쉬워질 뿐만 아니라, 알고리즘을 적용할 수 있기 때문에 프로그램의 성능 자체도 향상된다. 반대로 자료구조를 사용하지 않는다면 알고리즘도 사용할 수 없고 (대부분의 알고리즘은 특정 자료구조 위에서 동작한다) 코드도 매우 복잡해지며 데이터를 유연하게 다룰 수도 없게 될 것이다.
자료구조의 종류
자료구조는 크게 ‘선형 자료구조’와 ‘비선형 자료구조’로 나뉜다.

선형 자료구조는 데이터를 선형으로 연결하는 것으로, 대표적으로 리스트, 스택, 큐가 있다.
선형 자료구조는 리스트가 가장 기본이 되며, 스택과 큐는 여기에 몇 가지 특징을 추가한 것이다. 자료들 사이의 앞뒤 관계가 일대일이다.
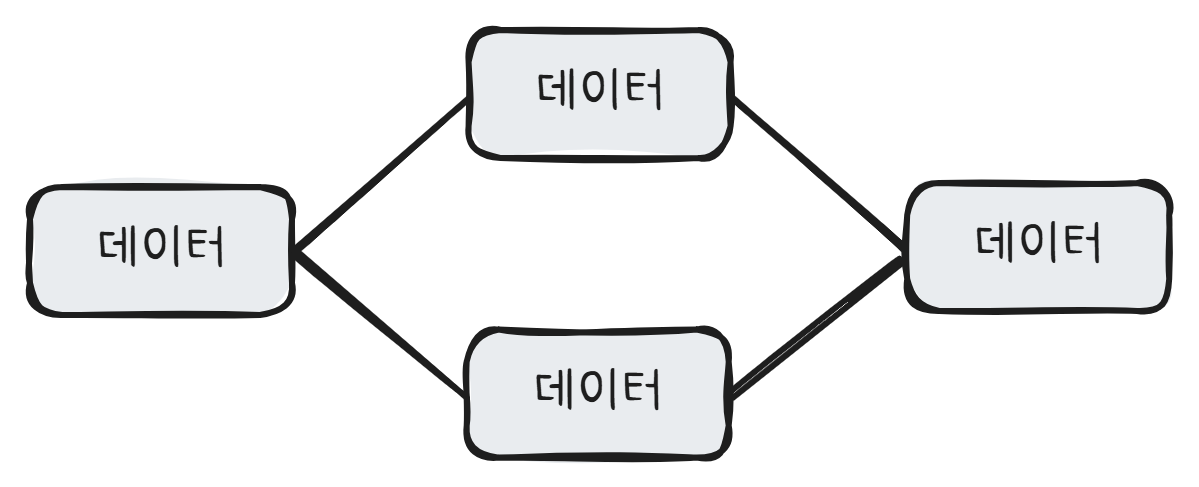
비선형 자료구조는 데이터를 비선형으로 연결하는 것으로, 대표적으로 트리, 힙, 그래프가 있다.
비선형 자료구조는 자료들 사이의 앞뒤 관계가 일대일이 아니다. 이를 보통 다대다 관계라고 부른다.
미리 알아야 할 개념
1. 시간 복잡도
위에서 말했듯 자료구조는 알고리즘과 관계가 깊다. 알고리즘은 프로그램의 성능을 높이기 위하여 코드를 더욱 효율적으로 작성하기 위한 것인데, 이런 알고리즘이 특정한 자료구조 위에서 동작하기 때문이다.
알고리즘의 성능은 연산 횟수가 얼마나 적느냐로 결정된다. 이와 관련하여 나오는 개념이 바로 시간 복잡도인데, 알고리즘의 수행에 걸리는 시간을 나타내 주는 지표이다.
예를 들어 C언어로 작성된 아래의 코드를 보자.
int algorithm(int n) {
int i = 0; // 1번
int sum = 0; // 1번
for (; i < n; i++) { // n * 2번
sum += i; // n * 1번
}
return sum;
}
위의 함수는 입력받은 파라미터 n의 값에 따라서 내부에서 반복문을 실행한다. 그렇다면 총 몇 번의 연산이 실행될까?
우선 int i = 0;에서 1번, int sum = 0;에서 1번의 연산이 실행된다. 그 다음 for문은 총 n번 반복되는데, 각 반복마다 i < n, i++, sum += i 가 각각 실행되므로 for문에서는 총 3n번의 연산을 한다고 볼 수 있다.
따라서 위의 함수에서 내부적으로는 총 3n + 2번의 연산이 발생한다고 볼 수 있다. 이것을 시간 복잡도 함수라고 부른다. 위의 함수는 넣는 값 n에 따라 3n + 2번의 연산이 발생하므로 시간 복잡도 함수가 3n + 2이다.
여기에서 가장 높은 차수를 가진 항만을 표기하는 방법을 빅-오 표기법이라고 한다. 예를 들어 위의 함수는 시간 복잡도 함수가 3n + 2이므로 최고차항은 3n이고, 계수를 생략하면 n이 된다. 따라서 위의 함수를 빅-오 표기법으로 나타내면 O(n)이 된다.
2. 노드
자료구조를 다루려면 먼저 노드에 대해서 알아야 한다. 노드란 자료를 저장하는 단위를 말한다.
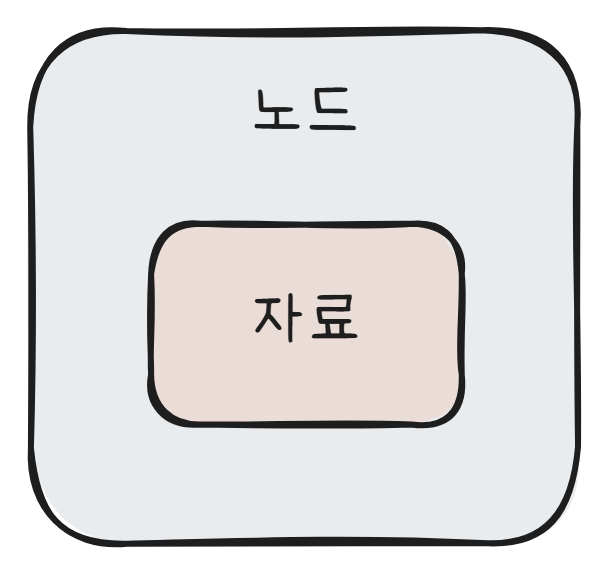
위와 같은 구조로 되어있는 것이 하나의 노드이고, 자료구조가 바로 이런 노드 각각이 다른 노드들과 연결되어 구조를 형성하는 것으로 구현된다. 노드는 일반적으로 클래스를 통해 구현되지만, C언어의 경우 클래스의 개념이 없기 때문에 구조체로 구현한다.
왜 자료를 그대로 사용하지 않고 노드를 사용하는 것일까? 그것은 노드 안에 여러 개의 자료를 담을 수 있기 때문이다. 예를 들어 아래의 코드를 보자.
int students[10];
이와 같은 식으로 배열을 만들면 students[] 각각에 하나의 int값만 담을 수 있다. 두 개 이상의 값을 하나의 자료에 넣는 것이 불가능하다.
typedef struct NodeType {
int number;
int age;
} Node;
하지만 이런 식으로 Node 구조체를 만들면 어떨까? struct NodeType으로 구조체가 만들어졌고, 이 구조체 안에는 number와 age의 두 개의 변수가 있다. 그리고 typedef를 통해서 struct NodeType을 Node라는 이름을 통해 쓸 수 있도록 만들었다.
Node students[10];
결과적으로 이런 코드를 사용할 수 있게 되는 것이다. 위에서 본 int students[10];와 달리 Node students[10];는 각각의 자료가 노드이기 때문에 두 개의 값(number, age)을 저장할 수 있다. 각각의 노드에 값을 몇 개 저장할지는 Node를 어떻게 만드느냐에 달려 있다.
배열 리스트 (Array List)
배열 리스트란 배열을 이용하여 만들어진 리스트를 뜻하며, 이때 리스트의 각 요소는 노드가 된다.
typedef struct NodeType {
int data;
} Node;
위처럼 노드를 먼저 정의한다. 위의 코드에서는 노드 안에 자료를 하나만 저장했지만, 여러 개를 저장해도 상관없다.
typedef struct ArrayListType {
int maxCount; // 최대 자료 개수 (배열의 크기)
int currentCount; // 현재 자료 개수
Node *pData; // 자료 저장을 위한 1차원 배열
} ArrayList;
그 다음으로는 위와 같이 배열 리스트를 만든다. 위의 코드에서 리스트를 저장하는 부분은 pData이다. pData는 Node의 포인터형으로, 이 포인터를 통하여 우리는 리스트에 저장된 노드에 접근할 수 있다.
나머지 maxCount와 currentCount는 단순히 리스트의 정보를 저장하는 역할을 하는 변수인데, 각각 배열이 가질 수 있는 최대 자료 개수와 현재 저장된 자료의 개수를 나타낸다.
Node와 ArrayList는 정의되었지만 아직 배열 리스트를 사용하기 위해서는 필요한 것들이 남아있다. 바로 배열 리스트를 다룰 수 있는 함수들을 정의하는 것이다. 우리는 리스트 생성, 자료 추가, 자료 삭제, 값 가져오기 등을 함수를 통해 수행한다.
리스트 생성 함수
ArrayList *createList(int count) {
ArrayList *pReturn = (ArrayList *)malloc(sizeof(ArrayList));
pReturn->maxCount = count;
pReturn->currentCount = 0;
pReturn->pData = (Node *)malloc(sizeof(Node) * count);
memset(pReturn->pData, 0, sizeof(Node) * count);
return pReturn;
}
자료 추가 함수
int addListData(ArrayList* pList, int position, int data) {
for (int i = pList->currentCount-1; i >= position; i--) {
pList->pData[position].data = data;
pList->currentCount++;
return 0;
}
}
자료 제거 함수
int removeListData(ArrayList* pList, int position) {
for (int i = position; i < pList->currentCount-1; i++) {
pList->pData[i] = pList->pData[i+1];
}
}
값 가져오기
int getListData(ArrayList* pList, int position) {
return pList->pData[position].data;
}
리스트 삭제
void deleteList(ArrayList* pList) {
free(pList->pData);
free(pList);
}
연결 리스트 (Linked List)
typedef struct NodeType {
int data;
strcut NodeType* pLink;
} Node;
typedef struct LinkedListType {
int currentCount;
Node headerNode;
} LinkedList;
리스트 생성 함수
LinkedList *createLinkedList() {
LinkedList *pReturn = (LinkedList *)malloc(sizeof(LinkedList));
memset(pReturn, 0, sizeof(LinkedList));
return pReturn;
}
값 가져오기
int getLinkedListData(LinkedList* pList, int position) {
Node *pCurrentNode = &(pList->headerNode);
for (int i = 0; i <= position; i++) {
pCurrentNode = pCurrentNode->pLink;
}
return pCurrentNode->data;
}
자료 추가 함수
int addLinkedListData(LinkedList* pList, int position, int data) {
Node *pNewNode = NULL;
Node *pPreNode = NULL;
pNewNode = (Node *)malloc(sizeof(Node));
pNewNode->data = data;
pPreNode = &(pList->headerNode);
for (int i = 0; i < position; i++) {
pPreNode = pPreNode->pLink;
}
pNewNode->pLink = pPreNode->pLink;
pPreNode->pLink = pNewNode;
pList->currentCount++;
return 0;
}
자료 제거 함수
int removeLinkedListData(LinkedList* pList, int position) {
Node *pDelNode = NULL;
Node *pPreNode = NULL;
pPreNode = &(pList->headerNode);
for (int i = 0; i < position; i++) {
pPreNode = pPreNode->pLink;
}
pDelNode = pPreNode->pLink;
pPreNode->pLink = pDelNode->pLink;
free(pDelNode);
pList->currentCount--;
return 0;
}
리스트 제거 함수
void deleteLinkedList(LinkedList* pList) {
Node *pDelNode = NULL;
Node *pPreNode = pList->headerNode.pLink;
while(pPreNode != NULL) {
pDelNode = pPreNode;
pPreNode = pPreNode->pLink;
free(pDelNode);
}
free(pList);
}
원형 연결 리스트
: 마지막 노드가 첫 번째 노드와 연결되어 원형을 이루는 구조.
※ 맨 처음 자료를 추가할 때 첫 노드가 다음 노드로 자신을 가리키도록 만들어야 한다.
※ 마지막 노드의 다음 노드는 첫 노드가 된다.
이중 연결 리스트
: 노드 사이의 연결이 양방향으로 이루어져 있는 구조.
※ 모든 노드가 두 개의 링크를 가진다. 하나는 앞에 있는 노드와, 다른 하나는 뒤에 있는 노드와 연결된다.
typeof struct NodeType {
int data;
struct NodeType* pLLink;
struct NodeType* pRLink;
} Node;
스택 (Stack)
LIFO (Last In First Out) : 가장 나중에 들어간 자료가 가장 먼저 나온다. (후입선출)
새로운 자료를 스택에 추가하는 과정을 push 연산이라고 한다. push 연산을 사용해 스택에 새로운 자료를 추가할 경우, 새로운 자료는 항상 기존 자료의 위쪽에만 저장할 수 있다.
스택에서 기존에 저장된 자료를 가져오는 과정을 pop 연산이라고 한다. 이 연산은 스택의 가장 위에 있는 자료를 제거하고 값을 가져온다.
배열 스택
typedef struct NodeType {
int data;
} Node;
typedef struct ArrayStackType {
int maxCount;
int currentCount;
Node *pData;
} ArrayStack;
스택 생성 함수
ArrayStack* createArrayStack(int size) {
ArrayStack* pReturn = NULL;
pReturn = (ArrayStack *)malloc(sizeof(Node) * size);
memset(pReturn, 0, sizeof(ArrayStack));
pReturn->maxCount = size;
pReturn->pData = (Node *)malloc(sizeof(Node) * size);
memset(pReturn->pData, 0, sizeof(Node) * size);
return pReturn;
}
push 연산
int isArrayStackFull(ArrayStack* pStack) {
int ret = 0;
if(pStack != NULL) {
if(pStack->currentCount == pStack->maxCount) {
ret = 1;
}
}
return ret;
}
int push(ArrayStack* pStack, int data) {
int ret = 0;
if(isArrayStackFull(pStack) == 0) {
pStack->pData[pStack->currentCount].data = data;
pStack->currentCount++;
ret = 1;
} else {
printf("Error: Stack full\n");
}
return ret;
}
pop 연산
int isArrayStackEmpty(ArrayStack* pStack) {
int ret = 0;
if(pStack != NULL) {
if(pStack->currentCount == 0) {
ret = 1;
}
}
return ret;
}
Node* pop(ArrayStack* pStack) {
Node *pReturn = NULL;
if(0 == isArrayStackEmpty(pStack)) {
pReturn = (Node *)malloc(sizeof(Node));
if (pReturn != NULL) {
pReturn->data = pStack->pData[pStack->currentCount - 1].data;
pStack->currentCount--;
} else {
printf("Error: 메모리 할당\n");
}
}
return pReturn;
}
peek 연산
Node* peek(ArrayStack* pStack) {
Node* pReturn = NULL;
if(pStack != NULL) {
if(isArrayStackEmpty(pStack) == 0) {
pReturn = &(pStack->pData[pStack->currentCount - 1]);
}
}
return pReturn;
}
배열 스택 삭제 함수
void deleteArrayStack(ArrayStack* pStack) {
if(pStack != NULL) {
if(pStack->pData != NULL) {
free(pStack->pData);
}
free(pStack);
}
}
연결 스택
typedef struct NodeType {
int data;
struct Node* pLink;
} Node;
typedef struct LinkedStackType {
int currentCount;
Node* pTop;
} LinkedStack;
스택 생성 함수
LinkedStack* createLinkedStack() {
LinkedStack *pReturn = NULL;
pReturn = (LinkedStack *)malloc(sizeof(LinkedStack));
memset(pReturn, 0, sizeof(LinkedStack));
return pReturn;
}
push 연산
int push(LinkedStack* pStack, int data) {
int ret = 0;
Node *pNode = NULL;
if(pStack != NULL) {
pNode = (Node *)malloc(sizeof(Node));
if (pNode != NULL) {
pNode->data = data;
pNode->pLink = pStack->pTop;
pStack->pTop = pNode;
pStack->currentCount++;
ret = 1;
} else {
printf("Error: 메모리 할당\n");
}
}
return ret;
}
pop 연산
int isLinkedStackEmpty(LinkedStack* pStack) {
int ret = 0;
if(pStack != NULL) {
if(pStack->currentCount == 0) {
ret = 1;
}
}
return ret;
}
Node* pop(LinkedStack* pStack) {
Node* pReturn = NULL;
if(pStack != NULL) {
if(isLinkedStackEmpty(pStack) == 0) {
pReturn = pStack->pTop;
pStack->pTop = pReturn->pLink;
pReturn->pLink = NULL;
pStack->currentCount--;
}
}
return pReturn;
}
peek 연산
Node* peek(LinkedStack* pStack) {
Node* pReturn = NULL;
if(pStack != NULL) {
if(isLinkedStackEmpty(pStack) == 0) {
pReturn = pStack->pTop;
}
}
return pReturn;
}
연결 스택 삭제
void deleteLinkedStack(LinkedStack* pStack) {
Node *pNode = NULL;
Node *pDelNode = NULL;
if(pStack != NULL) {
pNode = pStack->pTop;
while(pNode != NULL) {
pDelNode = pNode;
pNode = pNode->pLink;
free(pDelNode);
}
free(pStack);
}
}
큐 (Queue)
FIFO (First In First Out) : 먼저 들어간 자료가 먼저 나온다. (선입선출)
typedef struct NodeType{
int data;
} Node;
typedef struct ArrayQueueType {
int maxCount;
int currentCount;
int front;
int rear;
Node *pData;
} ArrayQueue;
큐 생성
ArrayQueue* createArrayQueue(int size) {
ArrayQueue *pReturn = NULL;
pReturn = (ArrayQueue *)malloc(sizeof(ArrayQueue));
memset(pReturn, 0, sizeof(ArrayQueue));
pReturn->maxCount = size;
pReturn->front = -1;
pReturn->rear = -1;
pReturn->pData = (Node *)malloc(sizeof(Node) * size);
memset(pReturn->pData, 0, sizeof(Node) * size);
return pReturn;
}
